Welcome to the Home Page of Measuring Pi Squaring Phi.
News Flash Update! Nov 30, 2018…
In keeping with the format of this web site, Measuring Pi Squaring Phi, I have now added a very simplified additional Proof 7 (a and b) for the Proof of Pi in the “Geometric Proofs of Pi” Menu Choice.
Proof 7 (a) “Pi Circumference Measurement” shows the reader how to use a manual Rotary Circle Cutter – an NT Model CL-100P adjustable 1+ meter diameter circle cutter with a very sharp carbon tool steel blade – to cut a 1,000.0 mm diameter circle and then measure the circle’s Pi circumference. No need to try to rent or buy an expensive ($100,000) and difficult to find CNC machine when using this Rotary Circle Cutter ($60).
Proof 7 (b) “Pi Math Proof” uses the same physically cut circle in Proof 7 (a) to show the reader a very simplified step by step math proof to draw the geometric proof of Pi = 4 / sqrt (Phi).
Those who want to jump right to Proof 7 (a and b), please go to Menu Choice “Geometric Proofs of Pi” at this web site and scroll down past Proofs 1 through 6, to Proof 7. Proof 7 is so simple a 14-year-old teenager studying Algebra 1 and Plane Geometry could do it with his/her left brain tied behind their back.
Those who want to continue reading about the use of a CNC machine to cut a 1 unit diameter circle to prove the Pi Circumference, continue reading from here.
The purpose of this web site, Measuring Pi Squaring Phi, is to show the reader how to easily solve for the true value of Pi. The web site is comprised of two main parts: (1) The physical measurement of a 1 unit diameter circle and its Pi circumference, and (2) The Geometric Proofs. You can start at either the physical measurements or the geometric proofs. They each enhance the other to prove the true value of Pi.
First, in the year 2017, we have the mechanical technology to easily create and physically measure the Pi circumference of a one-unit diameter circle cut by sophisticated and very accurate computer-controlled CNC machines. Out to at least 4 decimal places or more.
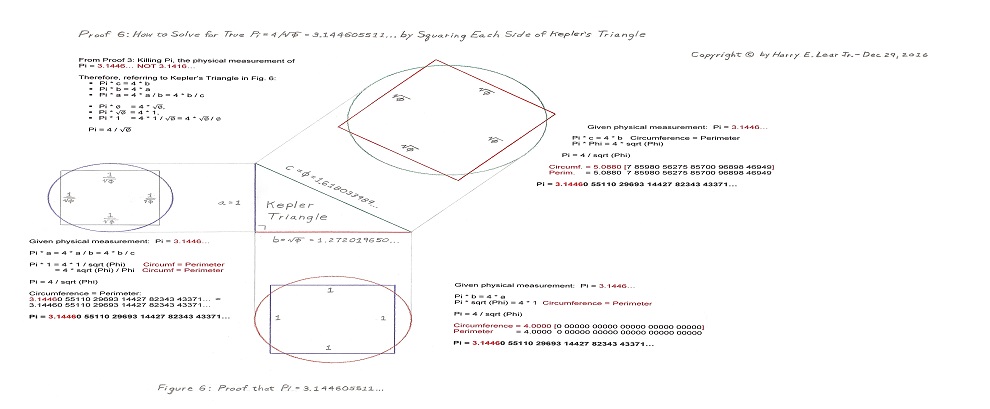
Second, I have discovered an important geometric and mathematical relationship between the sides of Kepler’s Golden Ratio Right Triangle which allows us to use our physically measured value of Pi to equate circumference to perimeter to prove that Pi is always reduced to 4 / sqrt Phi when “squaring” the circumference of each side of Kepler’s Triangle to the perimeter of its next largest side.
For the last several thousand years, no mathematician, not Archimedes, not Euler, not Euclid, not Sir Issac Newton, not Leibnitz, not Einstein (a physicist who wasn’t looking for the proof of Pi but used Pi = 3.1416…), or anybody else as far as I know — until now, at Measuring Pi Squaring Phi — has been able to present a proof for the true value of Pi.
Why?
One of the main stumbling blocks for today’s mathematicians is that they (a.) have not physically measured the Pi circumference of a one-unit diameter circle and thus do not know that Pi cannot possibly be 3.14159… , (b.) apparently no mathematician (until now) has discovered the special relationship between the “special squaring” of the sides of a Kepler Golden Ratio Right Triangle, and (c.) too many mathematicians using Archimedes’ polygon limit approach think it is OK to compute the tangent or arctangent of a right triangle whose short side is “curved” and not straight. If it’s not a straight side, it is not a right triangle and the notion of tan and arctan go out the window. Even using the calculus, it is a gross error to assume that you can compute the tan or arctan of a curved side, since then the curved triangle is not truly a triangle. It is this small amount of error (multiplied by all the 92 or however many polygon tangents around the inscribed and circumscribed circle you used in your erroneous “proof”) that reduces true Pi = 3.1446… to erroneous Pi = 3.1416… . In short, it is a gross error for mathematicians to use the tan or arctan of an arc of a circle and pretend it was not an arc. That is why the currently accepted, but erroneous, value of Pi = 3.1416… is too short by about .003 units.
As soon as you physically measure the Pi circumference of a one-unit diameter circle, you will throw away all your current math equations for Pi and see that they are in error at the 3rd decimal point. Next, contact your university engineering department and cut that one-unit diameter circle. Become an engineer AND a mathematician.
As you step through each section of Measuring Pi Squaring Phi, your goal should be to replicate what I have shown you at this Web Site. If you cut and measure your physical circle correctly, you should be able to get the same results that I have obtained. Plug your physical Pi value into my new — as far as I know — discovery of the “special squaring” of the sides of Kepler’s Golden Ratio Right Triangle, and you will also be able to prove the true value of Pi = 4 / sqrt Phi = 3.144605511… and out to 40 decimal places as I have done for each side of Kepler’s Triangle. If you have a super computer, you can carry Pi out to a million decimal places and the reduced equation for each squared side of Kepler’s Triangle will still be exactly correct: Pi = 4 / sqrt Phi.
Finally, a word about deductive and inductive reasoning, ordinal and cardinal numbers, physical measurements supporting math and science proofs, and so-called “circular logic.”
During the scientific and math process, both deductive and inductive reasoning is used to reach a logical conclusion.
DEDUCTIVE REASONING
Deductive reasoning starts with a GENERAL statement, or hypothesis, and examines the possibilities to reach a specific, logical conclusion. The scientific method uses deduction to test hypotheses and theories. In deductive inference, we hold a theory and based on it we make a PREDICTION of its consequences. That is, we predict what the observations should be if the theory were correct. We go from the general – the theory – to the specific – the observations.
Deductive reasoning usually follows steps. First, there is a premise, then a second premise, and finally an inference. A common form of deductive reasoning is the syllogism, in which two statements – a major premise and a minor premise – reach a logical conclusion. For example, the premise “Every A is B” could be followed by another premise, “This C is A.” Those statements would lead to the conclusion “This C is B.” Syllogisms are considered a good way to test deductive reasoning to make sure the argument is valid.
In order for deductive reasoning to be sound, the hypothesis must be correct. It is assumed that the premises are true. (Which is why researchers often jump back and forth between deductive and inductive reasoning.) Therefore, the conclusion is logical and true. In deductive reasoning, if something is true of a class of things in general, it is also true for all members of that class.
INDUCTIVE REASONING
Inductive reasoning is the opposite of deductive reasoning. Inductive reasoning makes broad generalizations from specific observations. Basically, there is data, then conclusions are drawn from the data.
In inductive inference, we go from the specific to the general. We make many observations, discern a pattern, make a generalization, and infer an explanation or a theory. In science and math, there is a constant interplay between inductive inference (based on observations) and deductive inference (based on theory), until we get closer and closer to the truth. The closer one’s deductions and inductions match objective reality, the closer one is to the truth.
Inductive reasoning has its place in science and math. Scientists use it to form hypotheses and theories. Deductive reasoning allows them to apply the theories to specific situations.
Note that deductive and inductive reasoning interact back and forth during the scientific process. Math theories are not only found by deductive reasoning, especially geometric and algebraic proofs. An interplay between deductive reasoning and inductive reasoning is very helpful in geometric proofs. Physical measurement is part of this deductive/inductive process and can lead to the truth of objective reality. Predictability is one of the hallmarks of truth, both in math and in science. Remember, math is simply a language about relationships in objective reality. Math is the language of science; it is not just some independent esoteric musing that has no relationship to objective physical reality.
PHYSICAL MEASUREMENTS
It is not true that math proofs or theorems cannot be proven by physical measurements. For example, in geometric proofs, physical measurements spoken with math (e.g. algebra) certainly do provide true proofs or theorems of mathematical hypotheses. The language of geometry speaks the truth or proves the non-proof of an hypothesis or theorem. For example, if a million mathematicians and scientists can replicate a math proof, whether physical or geometric, we can predict that another million scientists can also replicate said proof. That’s why NASA engineers — and engineers in other areas of science — step through “dress rehearsals” and tests of their equipment before they go “live.”
MEASURING PI SQUARING PHI
The web site Measuring Pi Squaring Phi uses the following:
- Inductive reasoning – Reasoning from the specific to the general by drawing ordinal relationships in geometric proofs for many examples of squaring the circumference of a circle to the perimeter of a square.
- Deductive reasoning – Reasoning from the general to the specific by hypothesizing that all circle circumferences can be “squared” to the perimeter of their respective square, and then proving it by (1) geometric proofs that show that only one true value of Pi can satisfy the hypothesis of the geometric proof, and (2) physically measuring the Pi circumference of a 1 unit diameter circle cut by a high tech CNC cutting machine.
- Interacting Deductive reasoning into the Inductive reasoning process AND the replication by other individuals of physical measurements that clearly refute the erroneous value of the currently accepted value of Pi = 3.141592654… while supporting the author’s new proof of Pi = 4 / sqrt Phi = 3.144605511… . In addition, the geometric proofs ALSO refute not only the currently accepted, but all other erroneous values of Pi while supporting the author’s new proof of Pi = 4 / sqrt Phi = 3.144605511… .
- Finally, the organizing of all the attributes of squared circles and their respective equal perimeter squares (circumference equal to perimeter) in a table that clearly shows five more universal constants other than Pi that are related to the Phi Golden Ratio phenomenon. Thus, proving that Pi and its relationship to the Phi phenomenon is only one of many universal constants related to the Phi phenomenon.
Regarding “circular logic,” a simultaneous proof of deductive and inductive reasoning, using ordinal values from geometric proofs, and cardinal values from physical measurement does not constitute “circular logic.” It constitutes simultaneous integrated logic in connection with objective reality. “Circular logic” is pulling a value out of thin air with no supporting inductive and/or deductive logic (or physically-replicated scientific measurement) and doing nothing else but just repeating the original hypothesis as the proof itself. I am not using “circular logic” to prove the true value of Pi = 4 / sqrt Phi = 3.144605511… . In summary, deductive reasoning is NOT the only method by which mathematicians can prove math theorems.
Thanks.
You can send me an email but I am not — at this time — allowing “online posting” at this web site. Nor am I interested in some huge debate. I am not running a chat room for everybody to vent their views (math or otherwise) but I retain the option of printing those emails that I think are positive for the readers.
Harry Lear