Welcome to the Geometric Proofs of Pi section of our Measuring Pi Squaring Phi web site.
News Flash Update! Nov 30, 2018…
Scroll down past Proof 6 in this section and view the latest simplified Proof 7 (a) Pi Circumference Measurement and Proof 7 (b) simplified Math Proof for the true value of Pi = 4 / sqrt (Phi).
This section is divided into two parts: (1) A Geometric picture of each Proof including an accompanying step by step summary of proof, and (2) A video of my stepping the reader through each step of each proof. The best way to view this section is to first do Part (1) View the Geometric Proof Photo, and then walk through Part (2), its video explanation. These geometric proofs are shown in chronological order of development as I learned more and more about how to discover the true value of Pi.
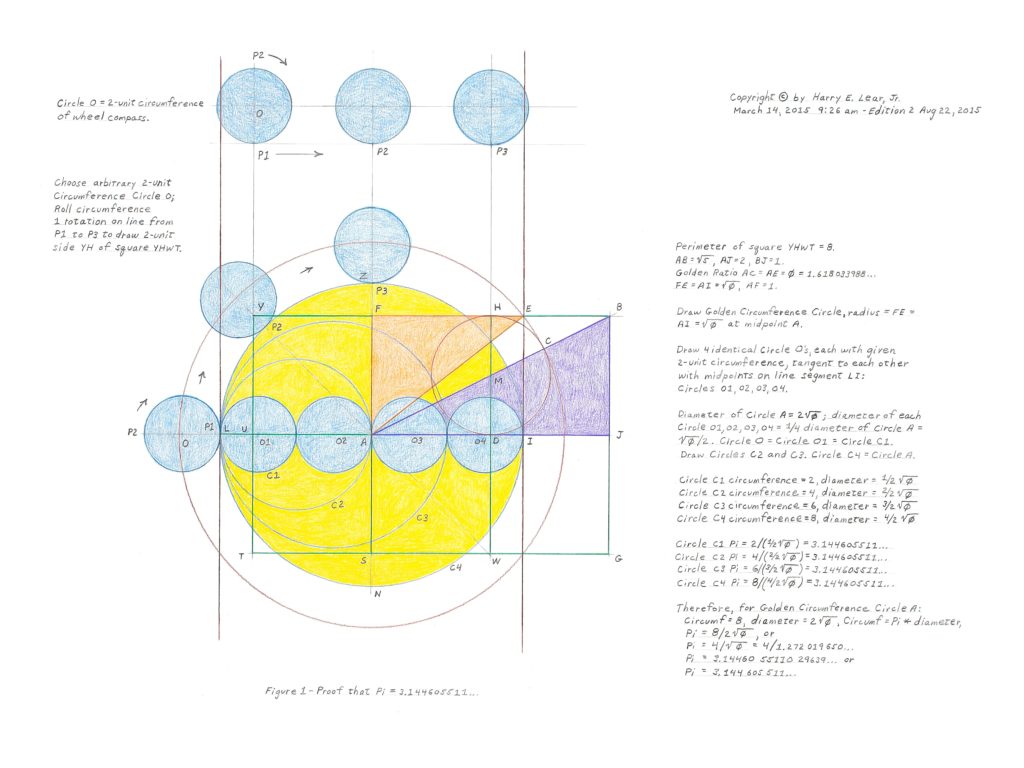
Note 1: For Geometric Proof 1, how was the blue circle with a given circumference of 2-units created? The real question is: how can one transfer the given 2-unit circumference of the blue circle onto a straight line which can then be used to draw the given 2-unit sided Square YHWT, which is then used in drawing Kepler’s Triangle and the rest of the drawing to prove True Pi?
I used an extra-sharp, carbon tool steel circular blade made by OLFA, Inc. and rolled it against a T-Square on a straight line on the drawing. For Proof 1, one revolution equals a given 2-units. My OLFA, Inc. rotary blade had an axle, so it was easy to roll against my T-Square after marking a point on the blade’s circumference to transfer one 2-unit revolution onto a straight line.
You can draw the given blue circle as a circle, of course, by simply drawing a circle around the rotary blade (allowing for the width of the pencil line) and then transferring the blue circle to the rest of the drawing with your compass. The above is true for both Proof 1 Fig 1 and Proof 2 Fig 2 using the same rotary blade except a 2-unit circumference is declared in Proof 1 Fig 1 and a Pi diameter and, therefore, Pi ^ 2 circumference is declared in Proof 2 Fig 2. These are ordinal given values, not cardinal measurements. For Proofs 4 and 6, you do not need to use given blue circles to start your geometric proof for Pi. Just create Kepler’s Golden Ratio Right Triangle and go from there.
Note 2: For those of you who are familiar with the proof of Archimedes’ Circles of Arbelos (“Arbelos” is Italian for the “shoemaker’s knife” due to its geometric shape), you can easily see in my Proofs 1 and 2 that the sum of the arcs of the top half of the 4 blue circles tangent across the diameter of the yellow circle equals the arc of the top half of the yellow circle. These arcs are the semi-circles of the blue and yellow circles. In fact, I have drawn multiple levels of Archimedes’ Arbelos Circles in Proof 1. In Proof 1 Fig. 1, the sum of the arcs of the top half of two blue circles equals the top half of Circle C2, and then the sum of the arcs of the top half of two Circle C2’s equal the top half of the yellow circle (which is the yellow circle’s semi-circle). As an aside, the area under each Arbelos blade equals the area above each Arbelos blade. You may want to review the Arblelos Circles on the Internet to understand why the diameters and circumferences of the 4 blue circles respectively equal the diameter and circumference of the yellow circle. With this information, we can easily calculate the true value of Pi as I have shown in each Proof.
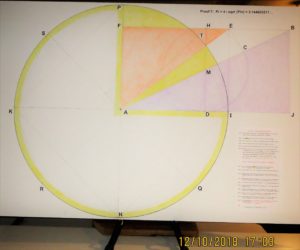
Geometric Proof 1 for True Value of Pi:
Walk-through for Geometric Proof 1 for the True Value of Pi
Note: A few readers have asked, “How do you know that the diameters of 4 blue circles fit exactly tangent across the diameter of the Big Yellow Circle in Proof 1 Fig 1?”
Answer:
Blue circle diameter = 2 / Pi, given where Circumf = 2, and diam = C / Pi, Proof 1 Fig 1,
Big Yellow circle diameter = 2 sqrt Phi, from Kepler’s Triangle Proof 1 Fig 1.
In Proof 1 Fig 1, we do not know yet what Pi is and so we ask, What is the value of Pi when the diameter of the Big Yellow Circle = 4 times the diameter of the Blue circle? The answer is:
2 sqrt Phi = 4 (2 / Pi), Solve for Pi
Pi = 4 / sqrt Phi,
Pi = 4 / 1.272019650… = 3.144605511…
Therefore, the diameter of 4 Blue circles fit exactly tangent across the diameter of the Big Yellow Circle in Proof 1 Fig 1 when Pi = 3.144605511… . And since Pi is a universal constant, not a variable, there is no need to look for another value of Pi.
Also, we can square the circumference of the Big Yellow Circle to the perimeter of Square YHWT, equate the two equations for C = P, and then solve for the value of Pi:
P, Perimeter of Square YHWT = 8, given in Proof 1 Fig 1,
C, Circumference of Big Yellow Circle = 2 Pi (sqrt Phi), from Kepler’s Triangle, Proof 1 Fig 1.
When C = P, what is the value of Pi?
Answer:
C = 2 Pi (sqrt Phi) = P = 8, Solve for Pi
Pi = 8 / (2 sqrt Phi),
Pi = 4 / sqrt Phi = 4 / 1.272019650… = 3.144605511…
Therefore, we have squared the circumference, C, to the perimeter, P, and equated C = P to solve for the only variable left, which is Pi = 4 / sqrt Phi. All of the above is clearly shown in Proof 1 Fig 1: (a) the Big Yellow Circle’s diameter is 4 times the diameter of the Blue circle, and (b) we have squared the Big Yellow Circle’s circumference to the perimeter of Square YHWT using the construction and sides of Kepler’s Golden Ratio Right Triangle.
Thanks for your questions. Time for you to step through the video of Proof 1 Fig 1:
Geometric Proof 2 for True Value of Pi:
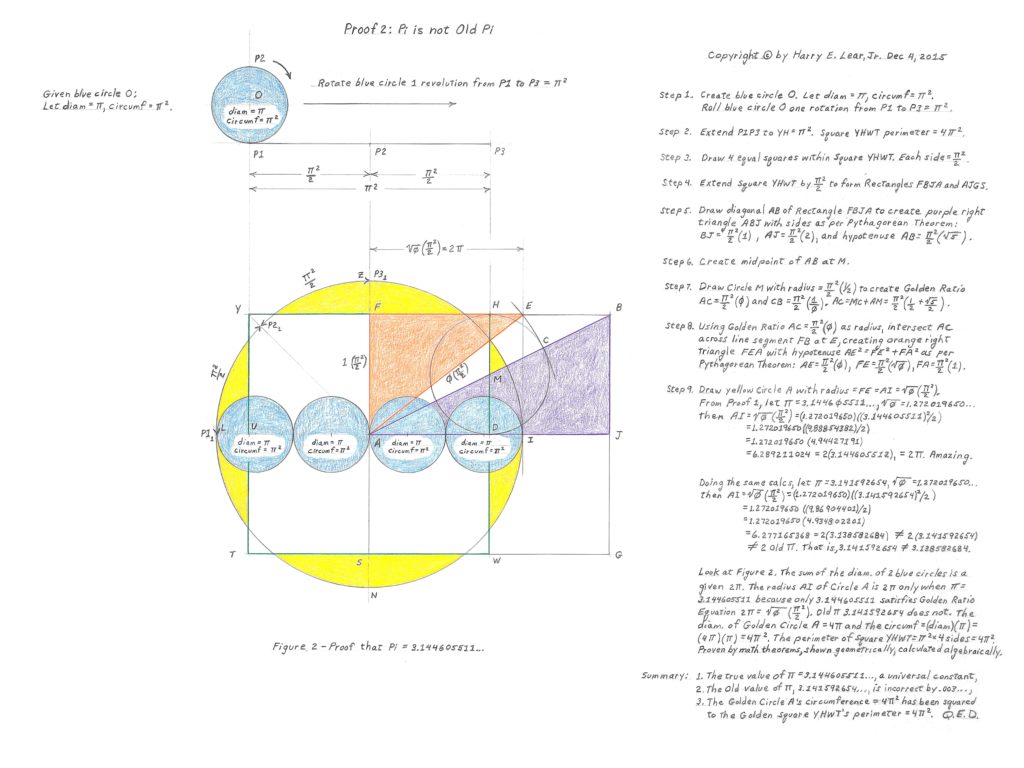
Geometric Proof 2 for True Pi
Walk-through for Geometric Proof 2 for the True Value of Pi
Note: A few readers have asked, “How do you know that the diameters of 4 blue circles fit exactly tangent across the diameter of the Big Yellow Circle in Proof 2 Fig 2?”
Answer:
Blue circle diameter = Pi, given where Circumf = C = diam x Pi = Pi^2, Proof 2 Fig 2,
Big Yellow Circle diameter = 2 sqrt Phi (Pi^2 / 2), from Kepler’s Triangle Proof 2 Fig 2.
In Proof 2 Fig 2, we do not know yet what Pi is – except that we really do know from Proof 1 Fig 1, but let’s continue with Proof 2 Fig 2 as if we didn’t know — and so we ask, What is the value of Pi when the diameter of the Big Yellow Circle = 4 times the diameter of the Blue circle? The answer is:
2 sqrt Phi (Pi^2 / 2) = 4 Pi, Solve for Pi
Sqrt Phi (Pi) = 4 ,
Pi = 4 / 1.272019650… = 3.144605511…
Therefore, the diameter of 4 Blue circles fit exactly tangent across the diameter of the Big Yellow Circle in Proof 2 Fig 2 when Pi = 3.144605511… . And since Pi is a universal constant, not a variable, there is no need to look for another value of Pi.
Also, we can square the circumference of the Big Yellow Circle to the perimeter of Square YHWT, equate the two equations for C = P, and then solve for the value of Pi:
P, Perimeter of Square YHWT = 4 Pi^2, given in Proof 2 Fig 2,
C, Circumference of Big Yellow Circle = 2 Pi (sqrt Phi) (Pi^2 / 2), from Kepler’s Triangle, Proof 2 Fig 2.
When C = P, what is the value of Pi?
Answer:
C = 2 Pi (sqrt Phi) (Pi^2 / 2) = P = 4 Pi^2, Solve for Pi
Pi (sqrt Phi) = 4,
Pi = 4 / sqrt Phi = 4 / 1.272019650… = 3.144605511…
Therefore, we have squared the circumference, C, to the perimeter, P, and equated C = P to solve for the only variable left, which is Pi = 4 / sqrt Phi. All of the above is clearly shown in Proof 2 Fig 2: (a) the Big Yellow Circle’s diameter is 4 times the diameter of the Blue circle, and (b) we have squared the Big Yellow Circle’s circumference to the perimeter of Square YHWT using the construction and sides of Kepler’s Golden Ratio Right Triangle.
Proof 2 Addendum 1 Jan 04, 2018
Notice that one of the key attributes of Proof 2 is that I have defined BOTH the given perimeter of the Square YHWT and the Kepler-derived ordinal value circumference of the Yellow Circle A in terms of Pi: the side of YHWT is a given Pi^2, and the Kepler Triangle side of sqrt (Phi) x Pi^2 / 2 is the given radius of Yellow Circle A. Both equations — the perimeter, P, of Square YHWT and the circumference, C, of Yellow Circle A — are true. We merely want to find the true value of Pi that satisfies the equality of P = C.
Therefore,
Perimeter, P, of Square YHWT = 4 x (Pi ^2),
Circumference, C, of Yellow Circle A = radius x 2 Pi = sqrt (Phi) x (Pi^2 / 2) x 2 x Pi, or
reducing, Circumference, C, = sqrt (Phi) x (Pi^3).
Therefore, when “squaring” C to equal P, the value of Pi must be the same for both sides of the equation 4 x (Pi ^2) = sqrt (Phi) x (Pi^3), so that the Perimeter, P, equals (is “squared” to) the circumference, C.
Solving for Pi, when P = C,
4 x (Pi^2) = sqrt (Phi) x (Pi^3), Perimeter = Circumference
4 = sqrt (Phi) x Pi, divide both sides by Pi^2
4 / sqrt (Phi) = Pi, divide both sides by sqrt (Phi)
4 / 1.272019650… = Pi, sqrt (Phi) = 1.272019650…
3.144605511… = Pi conclusion
Substituting the value of Pi = 3.144605511… in both equations for P = C, we get:
4 (3.144605511)^2 = 39.55417528… for perimeter of Square YHWT, and
1.272019650 (3.144605511)^3 = 39.55417528… for circumference of Yellow Circle A.
Everything balances on both sides of the equation P = C when Pi = 3.144605511… .
If, however, we substitute Pi = 3.141592654… in both equations for P = C, we get:
4 (3.141592654)^2 = 39.4784176… for perimeter of Square YHWT, and
1.272019650 (3.141592654)^3 = 39.44059321… for circumference of Yellow Circle A.
The same equations for P and C do not balance if we use Old Pi = 3.141592654… as Pi. P does not equal C, even though we are using the same true given equations for both P and C. That means Old Pi = 3.141592654… is WRONG! It also means that any other value for Pi other than Pi = 3.144605511… would also be wrong because there are not 2 values for Pi. Pi is a universal constant, not a variable. And Proof 2 shows why true Pi = 4 / sqrt (Phi) = 3.144605511… and no other value.
QED. H. Lear
Thanks for your questions. Time for you to step through the video of Proof 2 Fig 2:
Geometric Proof 4 for True Value of Pi:

Geometric Proof 4 for True Pi
Walk-through for Geometric Proof 4 for the True Value of Pi
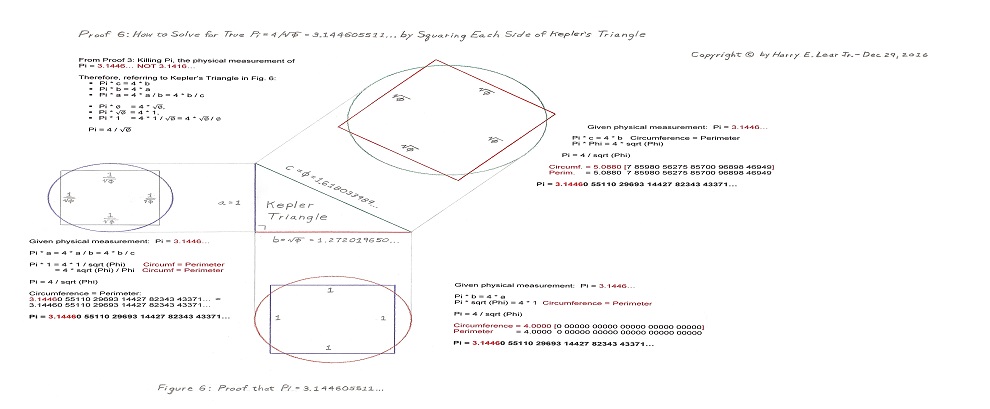
Geometric Proof 6 for True Value of Pi:
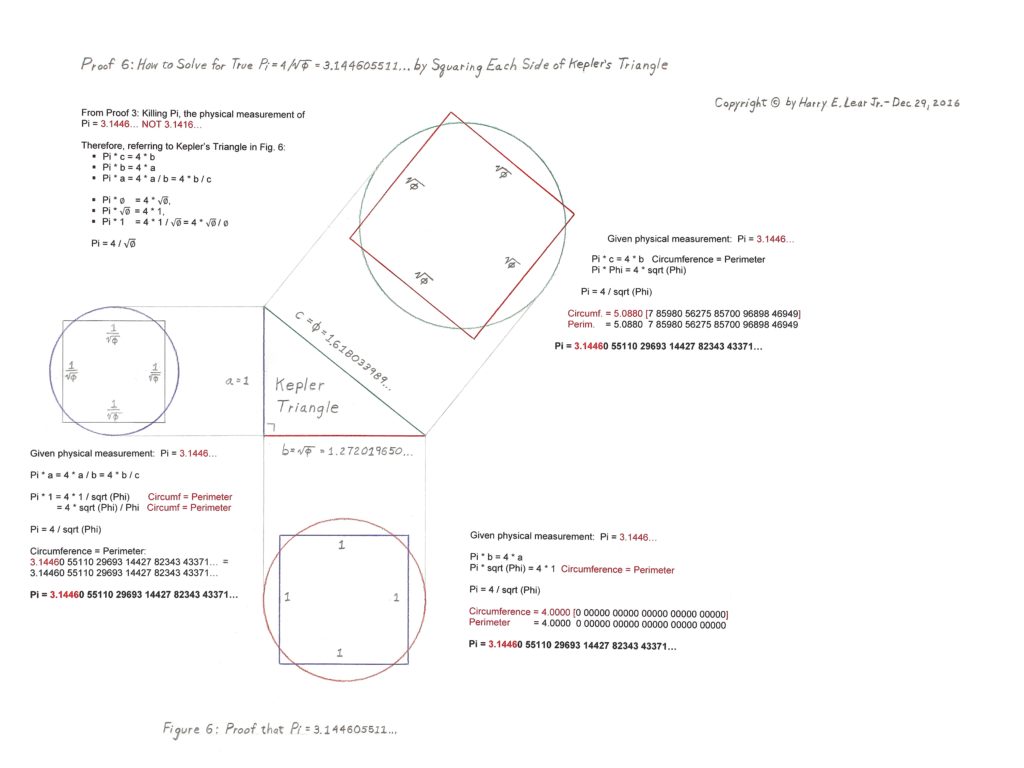
Geometric Proof 6 for True Pi
Note: Why Geometric Proof 6 is NOT circular reasoning.
The assumption that Proof 6 is a circular argument would be true if the Hypothesis only stated that Pi = 4 / sqrt Phi WITHOUT THE CONDITIONAL that the “Kepler Triangle-created circle and square remains squared.” Without this conditional of Circumference = Perimeter, one would simply be stating that Pi = 4 / sqrt Phi without any conditions. But Proof 6 explicitly states and shows that the “circumference of the circle must equal the perimeter of the square” – Pi x Phi = 4 x sqrt Phi – for the reduction of Pi = 4 / sqrt Phi = 3.144605511… to be true. That is why I show all the significant figures for Pi, Phi, and the sqrt Phi AND the same level (decimal places) of significant figures for circumference and perimeter.
Note that I compare significant figures of circumference and perimeter in Proof 6 from 2 to 40 decimal places (30 on the web site) and they match up digit by digit, thus proving that true Pi = 4 / sqrt Phi. Somebody with a super computer should carry out Proof 6 using 1 million or more significant figures (decimal places) for all the parameters and, if they did, I’m sure they would discover that Pi = 4 / sqrt Phi out to a million decimal places as the circumference equaled the perimeter.
NASA says they only use 40 significant figures for their Pi calculations (unfortunately, they’re using the wrong value of Pi = 3.141592654…) because this level of significant figures covers the diameter or size of our entire known universe. (NASA’s belief, not necessarily mine, as in who really knows the current size of our universe?)
Therefore, Proof 6 is actually testing any given value of Pi with the condition that the “circle is squared.” Any value prescribed for Pi — such as Old Pi = 3.141592654… that fails this “squared” condition of circumference = perimeter is rejected in Proof 6. Both True Pi and Old Pi at only 2 significant figures – 3.14… — passes the conditional “squared” test but Old Pi fails at the 3rd decimal place and thereafter.
Note that this special “squaring” of the sides of Kepler’s Triangle is true for all 3 sides, i.e. Pi times the longest side = 4 times the next longest side, etc. with a special ratio condition for the third side Case. Step through the narrative and you will see. Pi has been hiding in the Kepler Triangle for the last 2,000 years with, I suppose, nobody noticing all 3 Cases of the relationships shown in Proof 6.
Walk-through for Geometric Proof 6 for the True Value of Pi
Physical and Geometric Proof 7 for True Value of Pi
(Zoom in/out to view image)
Proof 7 for Pi
Walk-through for Proof 7(a) Physical Measurement of True Pi
Walk-through for Proof 7(b) Math Proof for True Pi
Proof 7 (a) and (b) Step by Step Physical and Math Proof for True Pi
Proof 7a – Physical Measurement of Pi
Step 1: Drawing table is flat and level. Calibrate beam compass and rotary circle
cutter to Starrett Engineering Tape Measure in millimeters. Use 3/8 – 1/2
inch thick x 40 inch x 60 inch poster board to cut Pi Circumference circle with
diameter = 1,000.0 mm and perform Proof 7 math proof.
Step 2: Draw yellow Circle A with 500.0 mm radius using beam compass.
Step 3: Draw Y-axis PN, mark 1,000.0 mm diameter with center at Point A, Circle A.
Step 4: Bisect PN, draw X-axis KI, mark 1,000.0 mm diameter of Circle A.
Step 5: Circumscribe (cut) groove around Circle A with NT CL-100P Rotary Cutter.
Step 6: Insert tape measure into cut groove around Circle A and measure the Pi
circumference of the 1,000.0 mm diameter, d, of Circle A. Wrap tape around
Circle A with hash marks facing inward against Circle A, not outward.
Otherwise you are adding the thickness of the tape measure to the
circumference. Circumference, C, = 3,144.6 mm, diameter, d, = 1,000.0 mm.
Therefore, Pi = C / d = 3,144.6 mm / 1,000.0 mm = 3.1446… .
Proof 7b – Math Proof for Pi = 4 / sqrt Phi = 3.144605511…
Step 7: Let circumference of yellow Circle A equal 8 units. Golden Ratio
Phi = 1.618033989… , sqrt Golden Ratio = 1.272019650…
Step 8: Draw chords PI = IN = NK = KP creating Square PINK inscribed within Circle A.
Step 9: Bisect Chords PI, IN, NK, KP of Square PINK, creating inscribed Octagon
PTIQNRKS with eight 1 unit Circle A Arcs PT = TI = IQ = QN = NR = RK = KS = SP.
Step 10: Place metal flat blade tape measure in cut groove of Circle A circumference to
transfer curved length of 1 unit Arc NQ to 1 unit straight line AD on x-axis.
Step 11: Draw Squares FHDA and HBJD with sides = 1 unit, creating Rectangle FBJA.
Step 12: Draw diagonal AB of Rectangle FBJA creating purple right Triangle ABJ with
Sides 1, 2, sqrt 5.
Step 13: At Diagonal Midpoint M, draw a 1 unit diameter Circle M to create Golden
Ratio Line AC = AM + MC = ((sqrt 5) / 2) + (1 / 2) = 1.618033989… called Phi
Step 14: Rotate AC to AE on Line FB to create orange Kepler Golden Ratio Right
Triangle FEA with sides FA = 1, FE = sqrt Phi, and AE = Phi.
Step 15: Use compass to transfer Kepler Triangle side FE = sqrt Phi to radius AI of
Circle A. Diameter KI of Circle A = 2 x sqrt Phi = 2 x 1.272019650…
Step 16: Since circumference, C, of Circle A = 8 units and diameter, d, of Circle A
= 2 sqrt Phi, then Pi = C / d = 8 / 2 sqrt Phi = 4 / sqrt Phi
= 4 / 1.272019650… = 3.144605511…
QED
Copyright © Nov 11, 2018 by Harry E. Lear, Jr.