Welcome to the Pi Math Proof section of this web site, Measuring Pi Squaring Phi.
News Flash Update! Nov 30, 2018…
Go to Main Menu Choice “Geometric Proofs of Pi,” and scroll down past Proof 6 in that section and view the latest simplified Proof 7 (a) Pi Circumference Measurement and Proof 7 (b) simplified Math Proof for the true value of Pi = 4 / sqrt (Phi).
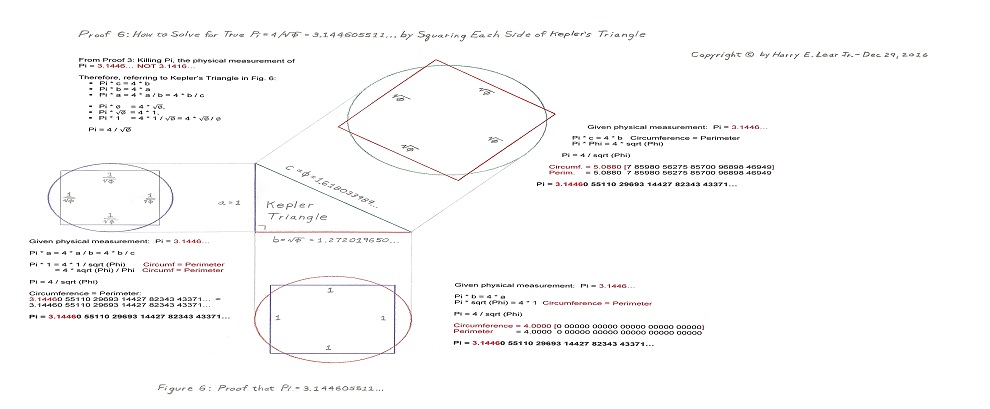
Now that we have physically measured the true value of Pi — see the three Pi Videos in the Pi Measurement section of this web site — it’s time to learn about my new discovery regarding the “special squaring” of each side of Kepler’s Golden Ratio Right Triangle to mathematically solve for the true value of Pi.
First, let’s get rid of the erroneous notion that (1) Pi must be a transcendental number, and (2) one cannot square the circumference of a circle to the perimeter of a square. The error made by many mathematicians is that they first claim that Pi = 3.141592654… by the old Archimedes polygon to circle limit equations which are only approximations and the use of erroneous built-in trig functions and, depending on how they invoked their “proof,” their erroneous Pi value = 3.141592654… is transcendental. That can be true, that their value of 3.141592654… is transcendental, BUT this value is not the true value of Pi. Then these same mathematicians make a quantum leap that, therefore, all proofs for the true value of Pi must be transcendental (even though theirs is wrong), and further, that nobody can use a straight edge and compass to square the circumference of a circle to the perimeter of a square. It is quite disingenuous to claim that Pi = 3.141592654… and that it is a transcendental number and, therefore, all proofs for Pi must be transcendental and not, for example, algebraic. This web site clearly shows that (1) by physical measurement, Pi cannot possibly be 3.14159… or even 3.141… and that it is at least 3.1446… , and (2) by algebra and geometric proofs, Pi does equal 3.144605511… (which I have carried out to 40 places), and, in addition, Pi is only one of many universal constants related to the Golden Ratio Phi phenomenon. All of the squared circle circumferences and their squares at this web site Measuring Pi Squaring Phi were drawn by using only straight edge and compass, including the squaring of a circle’s area to the area of a rectangle comprised of 8 Kepler Triangles. So let’s dump this notion that the proof of Pi must be “transcendental” (when we can show that it is algebraic) and that nobody can “square” the perimeter of a circle to a square.
So now, let’s find out what mathematician Johannes Kepler did not discover about his Golden Ratio Right Triangle back in the 16th century, i.e. how the sides of his 1, sqrt Phi, and Phi right triangle hold the simple key to unraveling the true value of Pi: (Play the video)